Introduzione
1) Pongo un quesito all’ing. Rugarli. Se si esegue un’analisi dinamica modale su un viadotto con sistemi di isolamento (che hanno coeff. di smorzamento viscoso equivalente > 5%) in testa alle sottostrutture, è giusto considerare per le verifiche di resistenza delle pile direttamente le sollecitazioni inviluppo che il software di calcolo riporta in output, (input di spettro scalato per T >= 0.8Tis)? In altre parole, può il diretto risultato di un’analisi dinamica modale (escludendo per semplicità effetti di interazione/deformabilità terreno-fondazioni, deformazioni anelastiche sezioni di connessione, effetti del II ordine, ecc.) essere rappresentativo per “estrarre” le sollecitazioni N, M, V, T ad esempio sulla sezione di spiccato di una pila (soprattutto nel caso di pile di altezza molto diversa fra loro)?
2) Sembrerebbe che i software di calcolo al momento disponibili non permettano di differenziare, almeno nelle analisi modali lineari, i “damping ratios” di tutti gli elementi presenti nel modello (in generale, le pile in condizioni di fessurazione, le fondazioni stesse, i terreni e gli apparecchi di appoggio stessi) e che il calcolo utilizzi lo stesso “damping ratio” fissato negli spettri con ramo scalato (quindi in funzione dei soli apparecchi di appoggio). La domanda: è sbagliato analizzare la pila e l’interazione terreno-fondazioni con un modello SDOF utilizzando in input gli scarichi “scalati” provenienti dall’impalcato (da analisi modale modello 3D)? E così poter calcolare, utilizzando per la pila e l’interazione suolo-fondazioni, differenti valori di “damping ratio”? La domanda mi appare ancora più pressante se nel viadotto ci sono pile molto alte.
L'argomento e le domande poste dal collega sono molto interessanti, per
rispondere però c'è bisogno di più spazio. Ecco quindi che qui do il mio punto
di vista sulla questione, rifacendo il punto sulla questione smorzamento anche per i non strettamente addentro ai problemi di calcolo e sviluppo.
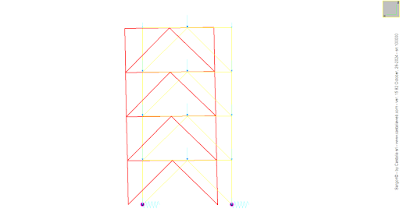 Due deformate modali. La seconda, in basso, rigorosamente disaccoppiata, la prima in alto, non proprio.
Due deformate modali. La seconda, in basso, rigorosamente disaccoppiata, la prima in alto, non proprio.
Lo smorzamento
E' importante dire che lo smorzamento in tutte le analisi dinamiche gioca un ruolo fondamentale. Una differenza nel valore di smorzamento può fare la differenza tra la vita e la morte, per una struttura. D'altro canto, sia per ragioni fisiche che per ragioni numeriche, la modellazione dello smorzamento è molto complicata e presenta aspetti incerti e di difficile valutazione.
Influiscono sullo smorzamento:
- La ampiezza delle oscillazioni.
- Le parti non strutturali e non modellate: partizioni, infissi, masse in moto attritivo.
- Lo smorzamento interno agli elementi strutturali, che può essere:
- Isteretico (legato a cicli di plasticizzazioni e scarichi), con o senza degrado ciclico
- Attritivo
- Legato a microfessurazioni o vere e proprie fratturazioni
- Lo smorzamento legato alla interazione delle fondazioni con il suolo.
- Radiation damping
- Lo smorzamento legato alla interazione della struttura con l'aria o coi i fluidi in cui è immersa.
- ....
Da un punto di vista numerico, lo smorzamento di gran lunga più usato è quello viscoso, in cui le forze di smorzamento sono direttamente proporzionali alla velocità. E' detto "equivalente" perché spesso è tarato in modo da comportare una dissipazione equivalente a quella che si vuole modellare.
Quando non si può, non si vuole o non si riesce a modellare in modo dettagliato lo smorzamento con appropriate leggi costitutive (smorzamenti 3 e 4, pur con le incognite legate alla modellazione del suolo, anche per mezzo di elementi concentrati), si ricorre allo smorzamento viscoso. Che è un "trucco" perché non tutti gli smorzamenti sono viscosi (ma qualcuno sì).
Si ricorre anche allo smorzamento viscoso per la modellazione di smorzamenti che sarebbe impossibile modellare esplicitamente (smorzamento 2 e 6). In letteratura tale smorzamento si chiama "inherent damping" o "unmodelled damping".
Se non si riesce a modellarli (per qualche ragione) anche gli smorzamenti 3, 4 e 5 e 6 vengono talvolta tenuti in conto con lo smorzamento viscoso.
In tutti i casi (anche i casi 3) la modellazione dello smorzamento (e del degrado ciclico) è complicata e presenta una incognita rispetto al reale comportamento sperimentale, in specie per le strutture esistenti, nelle quali non esistano dispositivi appositamente progettati allo scopo di dissipare energia.
La decomposizione modale
Perché si possa fare una analisi modale, il sistema deve essere disaccoppiabile. Se il sistema non è smorzato, è sempre disaccoppiabile. Se il sistema è smorzato, esso è disaccoppiabile solo quando lo smorzamento è viscoso (e basta) e la matrice dello smorzamento C presenta certe ben precise caratteristiche.
Quando lo smorzamento è tale da consentire il disaccoppiamento è detto "classico".
A livello di analisi modale, tre sono le tecniche classicamente in uso per disaccoppiare il sistema:
- Smorzamento alla Rayleigh : C = ɑM + 𝛽K.
- Smorzamento alla Caughey che è una estensione del precedente
- Smorzamento "modale" o alla Wilson-Penzien, o "light damping approximation"
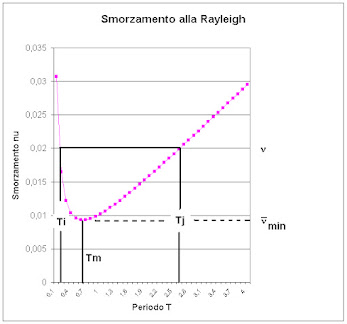
Lo smorzamento alla Rayleigh contente di specificare il valore di smorzamento relativo al critico solo di due modi (il cui smorzamento è imposto, o "collocato"). Gli smorzamenti degli altri modi derivano direttamente da una formula ben precisa, che dà lo smorzamento in funzione di ɑ di 𝛽 e delle frequenze dei due modi collocati. Il risultato è che lo smorzamento degli altri modi può essere completamente sbagliato, e in particolare, troppo alto. Quindi i modi ad alta frequenza possono essere smorzati via (damped out) dalla risposta, che può così venire a perdere parti importanti.
Lo smorzamento alla Caughey è computazionalmente molto più oneroso di quello alla Rayleigh, e comunque, dato che una struttura può avere dozzine di modi, può di fatto essere impiegato, ancora una volta, solo con precisione su alcuni.
Lo smorzamento alla Wilson-Penzien, di fatto ragiona in questo modo: a ogni modo estratto con i metodi normali, viene associato un certo smorzamento relativo al critico. Esiste una certa matrice di smorzamento viscoso C che dà luogo a questo risultato (tale C non è sparsa, il che ha ricadute sulle TH). Nelle analisi modali, tale matrice non è però calcolata, di fatto si utilizzano gli stessi modi. Da notare che la equazione del singolo oscillatore, ma viscosamente smorzato, presenta un periodo diverso da quello dell'oscillatore libero. Il termine per cui bisogna moltiplicare la pulsazione ⍵ è pari a sqrt(1-𝛎2), che, se lo smorzamento è piccolo, è praticamente pari a 1, ma che, se lo smorzamento è grande, può differire un po' più (con 𝛎 = 0.2 vale 0.98).
Questo ultimo tipo di smorzamento, è fattibile numericamente, ma non è detto che sia giustificato fisicamente: non è detto che il sistema sia veramente disaccoppiabile. In particolare, la presenza di smorzatori viscosi concentrati (tipicamente smorzatori in fondazione o isolatori), il sistema tipicamente non è disaccoppiabile.
Anche se si attribuisce agli elementi un certo smorzamento elementare, per esempio alla Rayleigh, per tener conto del diverso smorzamento in diverse parti della struttura, la matrice di smorzamento che si ottiene non è disaccoppiabile (cfr. infra).
Analisi a spettro di risposta (RS)
Lo smorzamento adoperato nella RS
Nella analisi a spettro di risposta viene normalmente impiegato uno spettro unico, con un dato smorzamento. Dello smorzamento si tien conto tramite la modifica dello spettro elastico con un certo smorzamento. Da quanto abbiamo visto prima, si capisce che tale assunzione coincide di fatto con uno smorzamento alla Wilson-Penzien in cui tutti i modi abbiano lo stesso smorzamento, quello dello spettro.
Tale assunzione è giustificata?
Se si fa una analisi modale con una struttura in cui siano presenti degli isolatori, ci saranno dei modi che sperabilmente saranno i primi, a periodo lungo, in cui la struttura tenderà a muoversi come corpo rigido sull'isolatore. Ci saranno poi dei modi a periodo più breve, sperabilmente ben distaccati dai primi, in cui la struttura si deformerà.
Nei primi modi, lo smorzamento da associare sarebbe quello degli smorzatori. Smorzamenti relativi al critico alti.
Nel secondi modi, lo smorzamento da associare sarebbe quello tipico della struttura, per esempio 5%.
Lo spettro di risposta da usare per questi modi, dovrà essere a rigore diverso. Non per la forma o per la PGA di ancoraggio (comunque assai discutibili), ma per lo smorzamento.
Dato che nella RS gli effetti dei modi vengono computati singolarmente, e poi combinati (con CQC o altro) a valle, nulla vieta di usare spettri con smorzamento diverso per modi diversi, ovvero spettri modali (potrebbe essere il metodo degli spettri di risposta modali). La norma al punto 7.10.5.3.2. dice che lo spettro di risposta elastico va ridotto con lo smorzamento del sistema di isolamento, solo per il campo di periodi corrispondente a T > 0.8sec. Il che è un modo per applicare due spettri di risposta diversi a seconda dei periodi. Più logico sarebbe applicare lo smorzamento in funzione della forma dei modi: per i modi che lasciano la struttura indeformata, lo smorzamento dell'isolatore, per i modi che la deformano, lo smorzamento del 5% o comunque quello "strutturale" (il 5% è uno smorzamento strutturale alto e tiene conto di un elevato livello di spostamento, ovvero di oscillazioni ampie). Nella speranza/esigenza che i due insiemi di modi non si presentino assieme.
Il problema è appunto che un qualche accoppiamento c'è quasi sempre. Se non ci fosse accoppiamento il periodo del modo traslazionale coinvolgente l'isolatore sarebbe quello dell'oscillatore di massa eguale alla massa totale della struttura e rigidezza pari alla sola rigidezza traslazionale dinamica degli isolatori. Se il periodo è più lungo, allora la struttura in qualche modo si deforma pure lei, e quindi vi è accoppiamento. La struttura non trasla rigidamente.
 Due deformate modali. La seconda, in basso, rigorosamente disaccoppiata, la prima in alto, non proprio.
Due deformate modali. La seconda, in basso, rigorosamente disaccoppiata, la prima in alto, non proprio.Quando sarebbe giustificato usare comunque un solo spettro, con uno smorzamento alto, nel caso di modellazione di struttura con smorzatori?
Sarebbe giustificato solo se il fattore di partecipazione dei modi coinvolgenti la struttura e che la vedano deformarsi, senza coinvolgimento degli isolatori, fosse molto basso, trascurabile, ovvero solo se ci fosse un disaccoppiamento totale, e effettivamente i modi deformativi della struttura fossero completamente ininfluenti.
Se ciò non avviene, assegnare a tali modi, non coinvolgenti gli isolatori, lo smorzamento degli isolatori non è a favore di sicurezza. Ma la norma consente di farlo solo per periodi maggiori di 0.8 secondi, come si è visto. Tali modi, con un isolatore, dovrebbero coinvolgere il solo isolatore.
Anche nel caso di modi misti, ovvero in cui si deformano sia le molle al piede simulanti gli isolatori, sia in qualche modo la struttura, la assegnazione di un unico smorzamento a quel modo pare discutibile.
Modi ad alta frequenza
I modi ad alta frequenza possono essere o no importanti.
Non sono importanti, ed anzi sarebbe meglio non considerarli, quando sono il risultato di atti di moto locali, favoriti e computati con una mesh localmente insufficiente. In questo caso la loro è una esistenza puramente numerica, nel senso che i modi locali, quando calcolati appropriatamente infittendo localmente la mesh, avrebbero forme e periodi diversi.
Sono importanti quando sono la corretta risposta di parti della struttura per le quali siano effettivamente presenti oscillazioni locali ad alta frequenza che, pur non essendo importanti globalmente, possono dare un contributo significativo localmente. E magari scatenare una crisi.
Nel primo caso, la loro sparizione per eccesso di smorzamento può essere un fatto positivo. Ciò può avvenire con lo smorzamento alla Rayleigh, che colloca solo i due modi più importanti, o con smorzamenti alla Wilson-Penzien variabili linearmente con la frequenza; può anche avvenire, nelle time history, quando il dT della analisi è paragonabile al T del modo in questione, e con certe tecniche numeriche piuttosto che altre (per esempio, il metodo Wilson-Θ, se il dT non è sufficientemente piccolo rispetto al periodo di un modo, lo fa sparire dalla risposta).
Dipende.
Time History Modale (THM)
La THM richiede il disaccoppiamento dei modi, e quindi impone che lo smorzamento sia classico:
- Alla Rayleigh
- Alla Caughey
- Alla Wilson-Penzien
Tutti questi smorzamenti esprimono condizioni sulla C globale assemblata e non usano smorzamento elementare.
Se ci sono altre fonti di smorzamento (isteresi, attrito), o se lo smorzamento non modellato non è del tipo indicato, la modale non si può fare e non si può nemmeno fare la THM. Però la THM continua ad avere valore per molte ragioni:
- E' utilizzabile per strutture lineari e con smorzamento classico (viscoso disaccoppiabile).
- Consente di studiare la energia elastica entrante nel sistema.
- Consente di prevedere picchi di risposta e di scegliere gli accelerogrammi (EDEM).
Time History con integrazione diretta, Lineare o Non Lineare (THL, THNL).
In questo caso i modi non servono. Però, serve un'altra cosa, che per la analisi di strutture realistiche non è meno importante: la sparsità di C.
Se C non è sparsa, la occupazione di memoria e il tempo di calcolo possono essere molto significativi o addirittura proibitivi. Le tecniche di integrazione (Newmark, Wilson-Θ), ricordo, perturbano la matrice di rigidezza (a ogni passo in campo NL), con contributi funzione della matrice delle masse M e della matrice di smorzamento C. Se questa non è sparsa, sono guai.
Ne consegue che, ad esempio, lo smorzamento alla Wilson-Penzien, che sarebbe auspicabile, non è di fatto utilizzabile (se non a un costo computazionale molto elevato quando ci sono tanti GDL) nelle THL e THNL, poiché conduce a una C non sparsa.
In tempi relativamente recenti (2016), nell'ambito delle THL e NL, è stato proposto lo smorzamento elementare, come tecnica atta a tener conto in modo puntuale del diverso smorzamento in diverse parti della struttura, in funzione del materiale e/o della zona (Puthanpurayil et al, 2016).
Non si sta parlando dello smorzamento isteretico o attritivo, seguito integrando le leggi costitutive nel tempo. Si sta parlando di un mezzo semplificato per tener conto dello smorzamento non modellato direttamente con le tecniche di integrazione della legge costitutiva. Di solito, uno smorzamento viscoso equivalente, che concorre all'assemblaggio della C globale.
Purtroppo, queste tecniche hanno mostrato limiti forti legati (Lee et al. 2023):
- Al fatto che si perde il significato fisico di quello che si sta facendo. Per avere smorzamenti globali decenti possono essere necessari smorzamenti elementari altissimi.
- Al fatto che non è accettabile che sia necessario smorzare anche gli atti di moto rigidi dell'elemento.
- Al fatto che la matrice C, benché sparsa, porti a sistemi non disaccoppiabili.
In tempi molto più recenti il meraviglioso lavoro di Lee (davvero straordinario), ha condotto a una completa ridefinizione del problema (Lee 2020).
Inizialmente le nuove tecniche hanno riguardato le tecniche classiche, con il particolare obiettivo di avere uno smorzamento globale alla Wilson-Penzien, ma con matrici sparse. La tecnica proposta nel 2020 fa uso di un assemblaggio completamente diverso e aggiunge altri nuovi gradi di libertà di appoggio. Lo smorzamento è modellato con "bell functions", che hanno generalità e flessibilità.
In un secondo tempo (Lee et al. 2023) l'approccio è stato esteso allo smorzamento elementare, risolvendo a quanto pare tutti i relativi problemi.
Al momento, pare di poter dire che l'approccio di Lee e del gruppo di studiosi neozelandesi è quanto di meglio esista per la modellazione dell'inherent damping viscoso.
Riepilogo smorzamenti
In presenza di smorzatori concentrati o di smorzamento isteretico o attritivo, non c'è mai la disaccoppiabilità, quindi tecniche modali non sembrano essere adeguate.
Allo stato attuale la situazione pare essere questa:
Smorzamento Disaccoppiabilità Sparsità Precisione Smorzamento
Rayleigh sì sì no
Caughey sì sì no
Wilson-Penzien sì no sì
Elementare Rayleigh(*) no sì no - perdita significato fisico
Elementare Bell Shaped (**) no no sì
Elementare Bell shaped (***) sì sì sì
(*) Ogni elemento ha il suo smorzamento alla Rayleigh
(**) Ogni elemento ha il suo smorzamento bell shaped, e l'assemblaggio è classico
(***) Ogni elemento ha il suo smorzamento bell shaped, e l'assemblaggio è alla Lee con nuovi gradi di libertà (Lee 2020)
Risposte ai quesiti dell'ing. Sigmund
Ora, chiarite un po' di cose, anche per utilità generale, posso provare a rispondere ai quesiti.
A mio parere dunque, a rigore la risposta alla domanda dell'ing. Carlo Sigmund numero 1) è "NO".
In presenza di smorzatori concentrati, la matrice di smorzamento C non ha la forma né dello smorzamento alla Rayleigh, né dello smorzamento alla Caughey, né di quello alla Wilson-Penzien. Pertanto una analisi "dinamica modale", fosse anche una THM e non una RS, non può dirsi un calcolo rigoroso.
Semplicemente, in presenza di smorzatori concentrati, il sistema non è disaccoppiabile.
A mio parere, se il sistema di smorzare i modi che presentino uno spostamento strutturale rigido (ammesso che esistano) con lo smorzamento dell'isolatore può essere un buon escamotage, io non lo adotterei in presenza di strutture molto importanti come forse un ponte con varie pile e per di più di diversa altezza.
Meno che meno adotterei uno smorzamento alto indiscriminatamente per tutti i modi. Se un modo presenta deformazione strutturale (indipendentemente dal suo periodo secondo me) lo smorzamento afds non può essere che quello della struttura. Se no, le corrispondenti azioni interne sono sottostimate.
In questi casi bisogna fare una integrazione nel tempo e quindi integrare il sistema.
Relativamente alla premessa del quesito 2), io non so dire cosa facciano i software perché il mio è un lavoro di sviluppo dei miei. Lo smorzamento "elementare" è stato inteso in letteratura come un modo per tener conto dello smorzamento non modellabile o "inerente" (non quello isteretico, non quello attritivo, che si modella integrando la legge costitutiva NL), in modo da differenziarlo da materiale a materiale e da zona a zona nella struttura. Tali tecniche presentano problemi perché è difficile mettere in relazione lo smorzamento degli elementi con quello globale, perché il sistema risulta non disaccoppiabile e perché si perde il significato fisico di quello che si sta facendo (Lee et al. 2023). Dato che l'assemblaggio di C elementari diverse (Ce) dà luogo a una C che accoppia il problema, le tecniche di smorzamento elementare non sono applicabili alla analisi modale (se non con speciali tecniche di assemblaggio introdotte dall'importante lavoro di Lee, e con la aggiunta di nuovi dof).
Lo smorzamento isteretico, quello attritivo, e quello degli smorzatori concentrati viscosi, non potrà mai, a mio parere, essere modellato in modo accurato con tecniche di decomposizione modale: è necessaria una analisi al passo che, a causa della natura del problema, non può che essere non lineare.
Le THNL rappresentano oggi quello che dobbiamo fare, per liberarci di lacci e lacciuoli che sono ormai non più necessari. Anche se, per moltissime ragioni, avremo comunque sempre e solo approssimazioni del comportamento reale e non precise simulazioni (magari apparentemente precise). In specie sulle costruzioni esistenti.
La risposta al quesito 2) (se ho capito bene) è che quello che si cerca di fare è di fatto disaccoppiare il moto facendo prima "alto" e poi "basso". Io semmai farei prima "basso" e poi "alto", ma non so se ho capito bene. Può darsi che questo in certi casi sia possibile, ma non credo che sia possibile in senso generale, in tutti i casi. Non vedo giustificazioni teoriche per fare una cosa del genere in generale, anzi vedo ostacoli legati all'accoppiamento. Forse si potrebbe procedere disaccoppiando quando una analisi modale mostri davvero che quando si deformano gli isolatori la struttura non si deforma (ma trasla a corpo rigido) e viceversa. Ma ho la sensazione che sia una situazione assai difficile da ottenere con rigore. In quel caso, uno in teoria potrebbe:
- studiare la risposta di un oscillatore semplice al segnale, tenendo conto della rigidezza locale dell'isolatore, della massa totale, e dello smorzamento locale.
- usare la risposta di questo oscillatore (la accelerazione in funzione del tempo) come segnale da applicare alla struttura su appoggi rigidi, e con il suo smorzamento inerente.
Ciò però implica assumere che quando si deforma l'isolatore la struttura resti rigorosamente indeformata il che penso sia raramente verificato.
La risposta al problema, capisco non troppo soddisfacente, secondo me è: THNL con:
- Modellazione dello smorzamento isteretico e attritivo per integrazione diretta delle leggi costitutive (includendo il degrado ecc.).
- Assemblaggio dello smorzamento viscoso degli smorzatori concentrati alla matrice C.
- Modellazione dell'inherent damping o con Rayleigh, o con smorzamento elementare nella modalità di Lee, per formare una matrice globale C che sia sparsa.
Le tecniche modali, temo, non sono sufficienti per modellare cose così complesse.
Comunque, lo studio procede e farò degli esperimenti numerici per ulteriore sicurezza. Le THNL sono attualmente un campo aperto di studio e ricerca, lo dimostrano l'articolo di solo un anno fa di Lee et al., che, mi pare, rivoluziona il campo.
Riferimenti
Lee C-L, (2020) Sparse proportional viscous damping model for structures with large number of degrees of freedom, Journal of Sound and Vibration, 478, 2020
Lee C-L., Chang T. L., Carr A J., (2023) Consistent Assembly method for elemental damping, Computers and Structures, 289, 2023
Puthanpurayl AM, Lavan O, Carr AJ e Dhakal RP (2016), Elemental Damping formulation: an alternative modelling of inherent damping in nonlinear dynamic analysis, Bul, Earth. Eng., 14(8)